环形公交路线上有 n 个站，按次序从 1 到 n  进行编号。我们已知每一对相邻公交站之间的距离a[i]，a[i]代表第i个车站到第i+1个车站之间的距离，其中a[n]为第n个车站到第1个车站之间的距离。环线上的公交车都可以按顺时针和逆时针的方向行驶。现在请你求出乘客从出发点x到目的地y之间的最短距离。

下图表示为有4个公交站，每一对相邻公交站之间的距离分别为1、2、3、4：

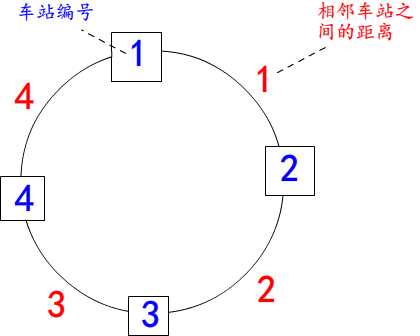
若起点为x=1, 目的地y=2，则最短距离为1。
解释：公交站1和2之间的距离是 1 或 9，最小值是 1。
 
输入：若起点为x=1, 目的地y=3，则最短距离为3。
解释：公交站1和3之间的距离是 3 或 7，最小值是 3。

输入：若起点为x=1, 目的地y=4，则最短距离为4。
解释：公交站1和4之间的距离是 6 或 4，最小值是 4。

第一行：一个正整数n（n<=1000)，表示有个公交车站。
第二行：有n个整数a[i]。a[i]代表每一对相邻公交站之间的距离（a[i]<=1000)。
第三行：两个整数x,y，分别代表出发点和目的地。

最短距离

6
1 2 3 4 2 1
5 2

4