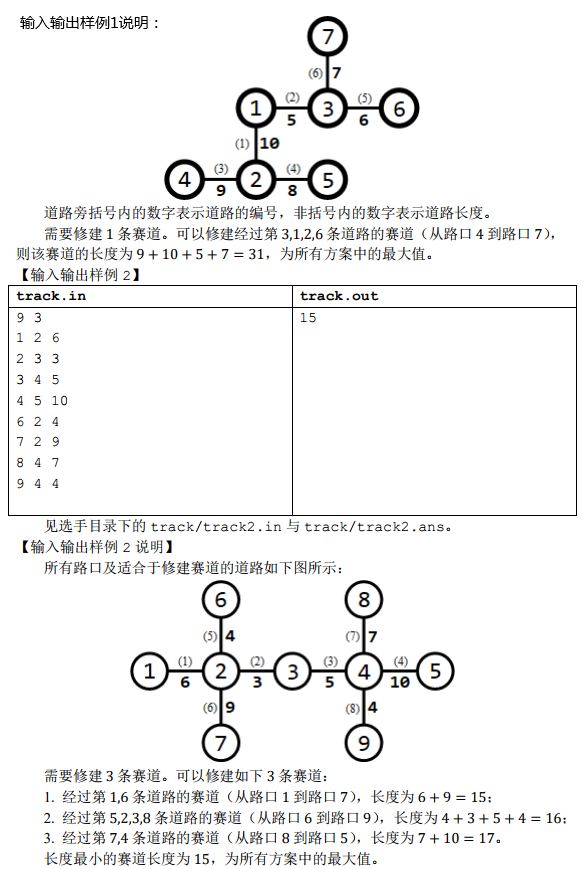
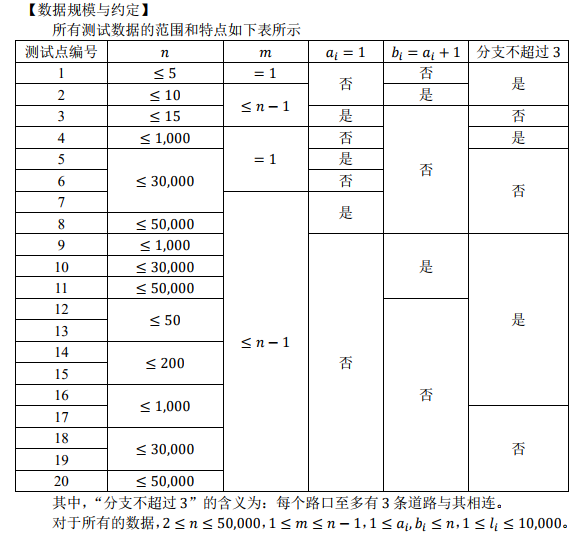
C 城将要举办一系列的赛车比赛。在比赛前，需要在城内修建 m 条赛道。
C 城一共有 n个路口，这些路口编号为 1,2,…,n，有 n−1 条适合于修建赛道的双向通行的道路，每条道路连接着两个路口。其中，第 i 条道路连接的两个路口编号为 a_i 和 b_i ，该道路的长度为 l_i 。借助这 n-1 条道路，从任何一个路口出发都能到达其他所有的路口。
一条赛道是一组互不相同的道路 e_1,e_2,…,e_k，满足可以从某个路口出发，依次经过 道路 e_1,e_2,…,e_k（每条道路经过一次，不允许调头）到达另一个路口。一条赛道的长度等于经过的各道路的长度之和。为保证安全，要求每条道路至多被一条赛道经过。
目前赛道修建的方案尚未确定。你的任务是设计一种赛道修建的方案，使得修建的 m 条赛道中长度最小的赛道长度最大（即 m 条赛道中最短赛道的长度尽可能大）

输入文件第一行包含两个由空格分隔的正整数 n,m，分别表示路口数及需要修建的赛道数。
接下来 n-1行，第 ii 行包含三个正整数 a_i,b_i,l_i ，表示第 i 条适合于修建赛道的道路连接的两个路口编号及道路长度。保证任意两个路口均可通过这 n−1 条道路相互到达。每行中相邻两数之间均由一个空格分隔。

输出共一行，包含一个整数，表示长度最小的赛道长度的最大值。

7 1
1 2 10
1 3 5
2 4 9
2 5 8
3 6 6
3 7 7

31